Задачи на движение

От чего зависит скорость бега человека

Помимо пола, возраста и дистанции, существуют факторы, влияющие на скорость бега, над которыми можно работать, которые возможно улучшить: 

• длина шага
• сила удара ступни о поверхность
• время контакта ступни с землёй
• быстрота сокращения мышечных волокон
• кислородный дефицит
• наклон туловища.

Исправляют, корректируют и улучшают эти факторы различные типы тренировок для бегунов: растяжка, специальные беговые упражнения на ноги, силовые упражнения на руки, корпус, пресс, спину, плиометрика, бег с отягощениями и так далее. Также на скорость влияет состояние организма в момент забега – вес тела, травмы и заболевания.

Максимальная скорость бега человека

Следующий фактор, который влияет на скорость, – дистанция. Большинство тренированных людей могут бежать со скоростью 15-20 км/ч, но не более одного километра. Дальше их скорость начнёт падать до 12-15 км/ч. Если говорить об элитных спортсменах, то на марафонских дистанциях скорость мужчин составляет 19-21 км/ч. Женские показатели в беге на 12-15% ниже.

Учитывая дистанцию, бегуны делятся на спринтеров (100-400 м), средневиков (800-3000 м), стайеров (5000-10000 м) и марафонцев, и системы их тренировок кардинально отличаются.

Самые высокие показатели скорости характерны для спринтерских дистанций: лучшие спортсмены преодолевают 100-метровку за 10-11 секунд, а 200 м за 19-20 секунд. Такое время спортсмены показывают в основном на соревнованиях, потому что даже на тренировках их скорость на 10-20% ниже максимальной.

У стайеров и марафонцев на первом плане – выносливость, способность держать стабильную скорость на протяжении длительного времени и разогнаться к финишу. У новичков на длинных дистанциях скорость составляет 9-12 км/ч, у тренированных людей – 16-18 км/ч.

Читайте по теме: Как развить и увеличить выносливость в беге

Быстрее всех пробежал 42 км 195 м Элиуд Кипчоге в октябре 2019 года – за 1 час 59 минут и 40,2 секунды. Для этого ему пришлось бежать всю дистанцию, сохраняя скорость 21,1 км/ч. Но этот рекорд не был засчитан, поскольку условия забега были почти “лабораторными” и нарушали марафонские правила.

Действующий мировой рекорд установил он же в 2018 году на марафоне в Берлине, пробежав его за 2 часа 1 минуту и 39 секунд.

Неоднократно спринтеров и стайеров пытались сравнить, и для этого учёные вычислили дистанцию, на которой их физическая форма может быть сопоставима – это 492 метра.

Для интереса можно взглянуть, как марафонец-любитель Искандер Ядгаров и спринтер-профессионал Рушан Абдулкадеров в 2018 году выясняли, кто из них будет быстрее на дистанции 450 м.

Наука и скорость бега

Ученые утверждают, что человек способен бежать со скоростью почти 65 км/ч. Новое исследование американских учёных о биологических пределах скорости предлагает по-новому посмотреть на биологию скорости человека.

Считается, что скорость ограничена силой, с которой конечности могут ударяться о поверхность во время бега. Элитные спортсмены могут прикладывать от 360 до 456 кг на одну конечность во время каждого шага. С такими цифрами легко поверить, что они бегут на пике своих возможностей. Но учёные выяснили, что это не так. Что конечности способны прикладывать гораздо большие силы к поверхности.

Ответ кроется в периодах времени контакта стопы с землёй. У элитных спринтеров это время составляет менее одной десятой секунды, а пиковые значения составляют менее одной двадцатой секунды.

Для исследования учёные использовали высокоскоростную беговую дорожку, развивающую скорость более 65 км/ч и способную измерять силу каждого шага. На ней спортсмены бежали назад, вперёд, прыгали на одной ноге. Оказалось, что во время прыжков на одной ноге на максимальной скорости сила, приложенная к поверхности, больше силы при беге на максимальной скорости на двух ногах на 30%.

Также выяснилось, что время соприкосновения ноги с поверхностью при беге вперёд совпадает во временем соприкосновения конечности при беге назад, при этом бег назад, конечно, медленнее. Это совпадение времени при двух очень разных видах активности указывает, насколько быстро мышечные волокна могут создавать силы, необходимые для того, чтобы бегун отрывался от земли во время каждого шага.

Новая работа показывает, что ограничения скорости бега устанавливаются ограничениями скорости сокращения самих мышечных волокон, а скорость сокращения волокон устанавливает предел того, насколько быстро конечность бегуна может прикладывать силу к поверхности бега.

Чтобы преодолеть биологические ограничения скорости, учёные из Гарварда придумали экзокостюм, который снижает метаболические затраты на бег и повышает мышечную производительность. Этот костюм лёгкий и плотно облегает тело. Он имеет приводной блок, который тянет за провода, выступающие в роли второй пары мышц-разгибателей бедра. Исследование показало, что помогая мышцам бедра, костюм влияет и на разгибание колена, и на прикладываемую ступнёй силу к поверхности.

На данный момент исследования продолжаются, чтобы ещё больше снизить метаболические затраты на бег. Еще один немаловажный аспект – доступность такого экзокостюма. Цель учёных – разработать портативную систему, чтобы польза от неё значительно снижала стоимость её ношения.

Есть версия, что скорость бега человека ограничена, потому что большую часть времени бега мы находимся в воздухе. А когда наши ноги касаются земли, у нас остается слишком мало времени, чтобы приложить силу к поверхности. Так, Усэйн Болт находится на земле 42-43% от общего времени шага, в то время как самые быстрые животные – гепард или лошадь – тратят две трети времени шага на контакт с землёй. Неужели, чтобы бежать быстрее, стоит бежать на четырех ногах?

Мировой рекорд Гиннесса для человека, бегущего 100 метров на четвереньках, улучшился с 18,58 секунды в 2008 году (первый год отслеживания записи) до 15,71 секунды в 2015 году. Исследователи сделали вывод на основе этих цифр, что к 2048 году человек на четвереньках сможет двигаться быстрее, чем человек, бегущий прямо!

Аналог «средней температуры» в механике

В каких случаях каверзно сформулированные условия задачи подталкивают нас к поспешному необдуманному ответу? Если говорится о «частях» пути, но не указывается их протяжённость, это настораживает даже мало искушённого в решении подобных примеров человека. А вот если в задаче прямо указывается на равные промежутки, например, «первую половину пути поезд следовал со скоростью. «, или «первую треть пути пешеход прошагал соскоростью. «, и далее подробно расписывается, как объёкт передвигался на оставшихся равных участках, то есть известно соотношение S₁ = S₂ = . = S_n и точные значения скоростей v_1, v_2, . v_n, наше мышление нередко даёт непростительную осечку. Считается среднее арифметическое скоростей, то есть все известные значения v складываются и делятся на n. В итоге ответ получается неверный.

Средняя скорость шага

Здравствуйте, дорогие читатели! С Вами на этой страничке я, Альберт! Сегодня врагом современного человечества считается гиподинамия.

А самым простым способом борьбы с ней является ходьба. Эта доступная физическая нагрузка помогает сбросить лишний вес, снять усталость после трудового дня, повысить выносливость и иммунитет.

Иначе недостаточная двигательная активность, которая обеспечивает людям функционирование всех мышечных, суставных и костных структур, может спровоцировать у них развитие серьезных патологических процессов. Например, у мужчин с возрастом — сердечную недостаточность, а у женщин после менопаузы — остеопороз.

При этом если человек хочет быть здоровыми, он должен постоянно активно регулировать свою двигательную функцию. Однако эта опция сугубо индивидуальна.

Ведь средняя скорость человека при ходьбе, при беге или прогулках на лыжах, значительно отличаются. Поэтому я хочу познакомить Вас с этими значениями, в каких пределах они колеблются и как связаны с состоянием здоровья человека.

Как рассчитать скорость бега

Скорость показывает, какое расстояние вы преодолеваете в единицу времени. Может измеряться в метрах в секунду или в километрах в час.

Скорость – первый критерий, главная мера для бегунов. Даже несмотря на то, что спортивные часы чаще фиксируют наш темп, чем скорость. При этом темп (pace) – величина, обратная скорости (speed). Темп измеряется в минутах на километр и показывает, сколько времени тратит человека на преодоление определенного расстояния.

Формула расчёта скорости:

Скорость (км/ч) = (расстояние/время в минутах)*60
Темп (мин/км) = время в минутах/расстояние

Формула расчёта скорости из показателя темпа:

Скорость = 60/темп (км/ч) или 50/3*темп (м/с)

Тренировочные планы к марафону и полумарафону. Скачайте и начните подготовку сегодня.

Сколько нужно ходить в день

Начинающим не стоит сразу идти на рекорды, допустимо проводить тренировки продолжительностью в 20-30 минут в день. В таком режиме можно заниматься 1-2 недели, наблюдая за состоянием организма и его возможностями. Постепенно нагрузка должна возрасти до часа, хотя отдельные индивидуумы готовы посвятить 2-3 часа и более по мере роста физической выносливости. Оптимальное расстояние для ходока колеблется от 5 до 7 км в день, это как раз около 10 тысяч шагов. Со временем ваш уровень общей физической тренированности возрастет и, возможно, вы решите перейти на бег или высокоинтенсивные интервальные тренировки (ВИИТ) . Измерять количество шагов или пройденное расстояние помогают приложения для мобильных телефонов или фитнес-гаджеты, которые фиксируют очень многие физические показатели, включая пульс и количество сожженных калорий, и даже время и качество сна.

Длина шага человека

Для высчитывания средней скорости пешехода надо знать длину шага. Она зависит от таких факторов как пол, рост, раса, вес, походка (манера), и может колебаться от 30 см до 1 метра. Но определена среднестатистическая длина, для мужчины она составляет 0,76 м, а средняя длина шага женщины – 0,67 м.

Существует формула для определения средней длины шага в зависимости от роста

Дл.Ш = P:4 + 0,37

где:

      Дл.Ш – длина шага (м)

      P – рост.

Таким образом, средний шаг человека ростом 1,79 м составляет: Дл.Ш = 1,79 : 4 + 0,37 = 0,82 м.

Практически длину шага человека можно измерять опытным путем. Для этого необходимо отмерять участок длиной 10 метров, пройти по нему, подсчитывая количество шагов. Затем 10 м разделить на это количество, и получим длину одного.

Допустим, пешеход проделал за 10 метров 13 шагов. Получаем: Дл.Ш = 10 : 13 = 0,77 м

Частные случаи нахождения средней скорости

Это задачи на нахождение средней скорости

Задачи простые, важно понять и запомнить формулу: Если участков пути было два, тогда Если три, то соответственно: *Как вы поняли, смысл таков: в знаменателе складываются отрезки времени, в числители суммируем расстояния пройденные за соответствующие им отрезки времени. Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 61 км/ч, а вторую половину времени – со скоростью 87 км/ч

В правительстве обращение пока не комментируют. Ограничить скорость в населенных пунктах во вторник попросили премьера глава комитета Совета Федерации по регламенту и организации парламентской деятельности Вадим Тюльпанов и член этого комитета, экс-глава ГАИ России Владимир Федоров. Авторы обращения уверены, что снижение разрешенного лимита с 60 до 50 км/ч позволит сократить количество ДТП и уровень смертности на дорогах, а также поспособствует

. Подробнее: «По оценке экспертов, при скорости автомобиля 50 км/ч с учетом времени реакции и тормозного пути расстояние, которое проходит автомобиль до остановки, составляет 28 метров, а при скорости 60 км/ч — 36.

1. Два одинаковых участка пути. Пусть первую половину пути тело двигалось со скоростью , а вторую половину пути — со скоростью . Требуется найти среднюю скорость движения тела.

• Пусть — общая длина пройденного пути. Тогда на первом участке пути тело двигалось в течение интервала времени . Аналогично, на втором участке пути тело двигалось в течение интервала времени .
• Тогда средняя скорость движения равна:

2. Два одинаковых интервала движения. Пусть тело двигалось со скоростью в течение некоторого промежутка времени, а затем стало двигаться со скоростью в течение такого же промежутка времени. Требуется найти среднюю скорость движения тела.

• Пусть — общее время пути. Тогда путь, пройденный телом в течение первой половины времени движения, равен: . Аналогично, путь, пройденный телом в течение второй половины времени движения, равен: .
• Тогда средняя скорость движения равна:

Решим напоследок задачу из Всероссийской олимпиады школьников по физике, прошедшей в прошлом году, которая связана с темой нашего сегодняшнего занятия.

Тело двигалось с, и средняя скорость движения составила 4 м/с. Известно, что за последние с движения средняя скорость этого же тела составила 10 м/с. Определите среднюю скорость тела за первые с движения.

Пройденный телом путь составляет: м. Можно найти также путь, который прошло тело за последние с своего движения: м. Тогда за первые с своего движения тело преодолело путь в м. Следовательно, средняя скорость на этом участке пути составила: м/с.

Задачи на нахождение средней скорости движения очень любят предлагать на ЕГЭ и ОГЭ по физике, вступительных экзаменах, а также олимпиадах. Научиться решать эти задачи должен каждый школьник, если он планирует продолжить свое обучение в вузе. Помочь справиться с этой задачей может знающий товарищ, школьный учитель или репетитор по математике и физике. Удачи вам в изучении физики!

Репетитор по физике на Юго-ЗападнойСергей Валерьевич

Мгновенная скорость движения материальной точки

Пусть положение материальной точки в пространстве задано радиус-вектором $\overline{r}$. При движении этой точки этот радиус-вектор изменяется по величине и направлению. Допустим, что положение материальной точки в момент времени $t_1$ задано при помощи вектора ${\overline{r}}_1$, в момент времени $t_2$ положение этой же точки определяет вектор ${\overline{r}}_2$.

Тогда за время $\Delta t=t_2-t_1$, рассматриваемая нами материальная точка совершает перемещение, равное:

Тогда предел отношения $\frac{\Delta \overline{r}}{\Delta t}$ при $\Delta t\to 0$ называют мгновенной скоростью ($\overline{v}$):

Из выражения (2) следует, что скорость определяют как производную от перемещения по времени:

Скорость — векторная величина. Вектор $\frac{\Delta \overline{r}}{\Delta t}$ — это секущая для траектории движения точки. Вектор скорости является касательным к траектории (в соответствующей точке) движения тела.

В проекциях на оси декартовой системы координат вектор скорости записывают как:

где $\overline{i}$; $\overline{j}$; $\overline{k}$ — единичные векторы осей X, Y, Z; $v_x=\frac{dx}{dt};;v_y=\frac{dy}{dt};;\ v_z=\frac{dz}{dt}$. При этом модуль скорости найдем как:

Элементарный путь ($\Delta s$) в общем случае не равен модулю элементарного перемещения ($\left|\Delta \overline{r}\right|$), но если рассматривать отрезки пути и перемещения при $\Delta t\to 0$, то различие между этими параметрами будет тем меньше, чем ближе $\Delta t$ к нулю, поэтому можно считать, что:

Единицей скорости является скорость такого движения, при котором перемещение точки в единицу времени равно единице длины:

В Международной системе единиц (СИ) единицей измерения скорости (в том числе и средней скорости) является метр в секунду:

Что влияет на скорость пешехода

Скорость пешехода зависит от множества факторов. Вот некоторые из них: 

• возраст — маленькие дети и люди преклонных лет ходят намного медленнее, нежели обычный трудоспособный человек
• физическая подготовка и состояние здоровья пешехода
• удобство одежды и обуви. Надеюсь, никто не станет спорить с тем, что женщина на высоких каблуках и женщина в кроссовках будут передвигаться с кардинально разной скоростью
• качество покрытия дороги, по которой идет человек;
• скорость изменяется от того, двигается человек по пересеченной местности или по тротуару
• ученые отмечают, что скорость жителей густонаселенных пунктов ниже, нежели тех, кто передвигается по безлюдной местности. 

Формулы для равноускоренного движения

Формула для скорости при равноускоренном движении:

v=v+at.

Здесь v — начальная скорость тела, a=const — ускорение.

Покажем на графике, что при равноускоренном движении зависимость v(t) имеет вид прямой линии.

​​​​​​​

Ускорение можно определить по углу наклона графика скорости. На рисунке выше модуль ускорения равен отношению сторон треугольника ABC.

a=v-vt=BCAC

Чем больше угол β, тем больше наклон (крутизна) графика по отношению к оси времени. Соответственно, тем больше ускорение тела.

Для первого графика: v=-2 мс; a=,5 мс2.

Для второго графика: v=3 мс; a=-13 мс2.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

По данному графику можно также вычислить перемещение тела за время t. Как это сделать?

Выделим на графике малый отрезок времени ∆t. Будем считать, что он настолько мал, что движение за время ∆t можно считать равномерным движением со скоростью, равной скорости тела в середине промежутка ∆t. Тогда, перемещение ∆s за время ∆t будет равно ∆s=v∆t.

Разобьем все время t на бесконечно малые промежутки ∆t. Перемещение s за время t равно площади трапеции ODEF.

s=OD+EF2OF=v+v2t=2v+(v-v)2t.

Мы знаем, что v-v=at, поэтому окончательная формула для перемещения тела примет вид:

s=vt+at22

Для того, чтобы найти координату тела в данный момент времени, нужно к начальной координате тела добавить перемещение. Изменение координаты в зависимости от времени выражает закон равноускоренного движения.

Сколько калорий позволяет сжечь ходьба

Это интересно: жиросжигающий эффект ходьбы можно значительно усилить в разы. Для этого нужно проснуться утром чуть раньше, ничего не есть, выпить достаточно воды (ни в коем случае не пить чай или кофе с сахаром), одеться и отправляться на энергичную прогулку в течение 30 минут.

Во время такой ходьбы натощак , организм будет сжигать большое количество жира, потому что находится в состоянии голода. За 8-10 часов ночного сна наше тело успевает израсходовать практически все запасы энергетического вещества гликогена и поэтому вынуждено сжигать жир для выработки энергии

Важно помнить, что чем больше и крупнее человек, тем больше калорий он расходует в принципе. Например, человек весом в 70 кг за путь в 10 тысяч шагов будет терять 245 кал, а ходок весом в 50 кг сожжет всего 175 кал

Формула расчета сжигаемых калорий при ходьбе: количество шагов × длина шага в метрах × 0,0005 × вес человека

Для тех, кто затрудняется определить длину шага, уместно применить в расчетах среднестатистический показатель: 1 шаг = 0,7 метра. Утяжеления в виде груза на спину помогут увеличить расход калорий, то же происходит и с возрастанием интенсивности занятий. В целом при ходьбе необходимо опираться не на расчет потерянных калорий , а на изменение состава тела и увеличение выносливости. Эти показатели более адекватно передают картину оздоровления.

Пример решения задачи

Теперь, когда мы рассмотрели физические основы кинематики, пора закрепить знания на практике и решить какую-нибудь задачу. Причем, чем быстрее, тем лучше.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы. 

Решим такую задачу: точка движется по окружности радиусом 4 метра. Закон ее движения выражается уравнением S=A+Bt^2. А=8м, В=-2м/с^2. В какой момент времени нормальное ускорение точки равно 9 м/с^2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.

Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.

Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.

Равноускоренное движение

Равноускоренное движение — это движение, при котором вектор ускорения не меняется по модулю и направлению. Примеры такого движения: велосипед, который катится с горки; камень брошенный под углом к горизонту. Равномерное движение — частный случай равноускоренного движения с ускорением, равным нулю.

Рассмотрим случай свободного падения (тело брошено под уголом к горизонту) более подробно. Такое движение можно представить в виде суммы движений относительно вертикальной и горизонтальной осей.

В любой точке траектории на тело действует ускорение свободного падения g→, которое не меняется по величине и всегда направлено в одну сторону. 

Вдоль оси X движение равномерное и прямолинейное, а вдоль оси Y — равноускоренное и прямолинейное. Будем рассматривать проекции векторов скорости и ускорения на оси.

Сложение скоростей

Скорости движения тела в различных системах отсчёта связывает между собой классический
закон сложения скоростей.

Скорость тела относительно неподвижной системы отсчёта равна сумме
скоростей тела в подвижной системе отсчёта и самой подвижной системы
отсчёта относительно неподвижной.

Например, пассажирский поезд движется по железной дороге со скоростью 60 км/ч.
По вагону этого поезда идет человек со скоростью 5 км/ч. Если считать железную
дорогу неподвижной и принять её за систему отсчёта, то скорость человека относительно
системы отсчёта (то есть относительно железной дороги), будет равна сложению
скоростей поезда и человека, то есть

60 + 5 = 65, если человек идёт в том же направлении, что и поезд

60 – 5 = 55, если человек и поезд движутся в разных направлениях

Однако это справедливо только в том случае, если человек и поезд движутся по одной линии.
Если же человек будет двигаться под углом, то придётся учитывать этот угол, вспомнив о том,
что скорость – это векторная величина.

А теперь рассмотрим описанный выше пример более подробно – с деталями и картинками.

Итак, в нашем случае железная дорога – это неподвижная система отсчёта.
Поезд, который движется по этой дороге – это подвижная система отсчёта.
Вагон, по которому идёт человек, является частью поезда.

Скорость человека относительно вагона (относительно подвижной системы отсчёта) равна 5 км/ч.
Обозначим её буквой _Ч.

Скорость поезда (а значит и вагона) относительно неподвижной системы отсчёта
(то есть относительно железной дороги) равна 60 км/ч. Обозначим её буквой
_В. Иначе говоря, скорость
поезда – это скорость подвижной системы отсчёта относительно неподвижной системы отсчёта.

Скорость человека относительно железной дороги (относительно неподвижной системы отсчёта)
нам пока неизвестна. Обозначим её буквой .

Свяжем с неподвижной системой отсчёта (рис. 1.7) систему координат ХОY,
а с подвижной системой отсчёта – систему координат X_ПО_ПY_П
(см. также раздел ).
А теперь попробуем найти скорость человека относительно неподвижной системы отсчёта,
то есть относительно железной дороги.

За малый промежуток времени Δt происходят следующие события:

• Человек перемещается относительно вагона на расстояние _Ч
• Вагон перемещается относительно железной дороги на расстояние _B

= _Ч + _B

Это закон сложения перемещений. В нашем примере перемещение человека
относительно железной дороги равно сумме перемещений человека относительно вагона и
вагона относительно железной дороги.

Рис. 1.7. Закон сложения перемещений.

Закон сложения перемещений можно записать так:

_ЧB

Скорость человека относительно железной дороги равна:

 =  / Δt

= _Ч + _B

то

Скорость человека относительно вагона:

ΔЧ = Ч / Δt

ΔB = B / Δt

 = ΔЧ + ΔB

сложения скоростей
Скорость тела относительно неподвижной системы отсчёта равна сумме скоростей тела в подвижной системе отсчёта и скорости самой подвижной системы отсчёта относительно неподвижной.

Средняя скорость автомобилей на МКАД

Определяет степень использования пробега автомобиля с грузом.

При работе автомобиля на линии различают пробеги: общий, с грузом, холостой и нулевой.

Пробег с грузом является производительным пробегом.

где: Sгp — пробег с грузом, км; Sо.пр — общий пробег автомобиля, км.

Пример. Общий пробег автомобиля за день составил 320 км, с грузом — 244 км. Определить КИПр.

Решение.

Величина коэффициента использования пробега зависит от размещения пунктов погрузки и разгрузки, характера грузопотоков и организации диспетчерской службы на линии. Водители-новаторы добиваются сокращения непроизводительных пробегов за счет перевозки попутных грузов. Например, при перевозке сахарной свеклы с поля на сахарный завод они используют обратные рейсы для перевозки на поля минеральных удобрений.

Решение.

Примеры задач с решением

Пример 1

Задание: Движение точки M (рис.1) задано уравнением: $x=2t^2-4t^3$(м). Начало движения при $t=0$ c. Каким будет направление движения этой точки по отношению к оси X при 1) $t_1$=0,25 c 2) $t_2$=0,5 c.

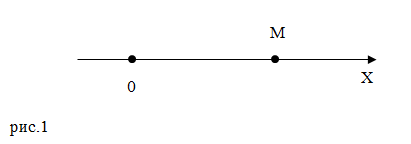
Решение: Точка движется по оси X, следовательно, скорость найдем как:

\

Подставим выражение $x(t)$ заданное в условии задачи в формулу (1.1), получим функцию $v_x(t)$:

\

Для того чтобы определить направление скорости в конкретный момент времени подставим соответствующий момент времени в (1.2) и сравним полученный результат с нулем:

\

\[v_{x2}\left(t_2=0,5\ с\right)=4\cdot 0,5-12{\left(0,5\right)}^2=-1\ (\frac{м}{с})Ответ: 1) $v_{x1}\left(t_1=0,25\ с\right)$ направлена по оси X. 2) $v_{x2}\left(t_2=0,5\ с\right)$
направлена против оси X.
   

Пример 2

Задание: Дан закон движения материальной точки: s$=At^2+Bt$ ($A>0$ и $B>0$ — постоянные величины). Сравните среднюю скорость, полученную при использовании формулы:

\

и среднюю скорость, вычисленную как среднее арифметическое начальной и конечной скоростей в интервале времени $\left$.

Решение: Найдем величину средней скорости, используя определение:

\

и уравнение движения:

\

Для момента времени $t’\ $ имеем:

\

Получим уравнение скорости $v\left(t\right),\ $используя формулу:

\

При $t=0$ мгновенная скорость рассматриваемого нами движения равна:

\

Конечная скорость при $t=t’$:

\

Найдем среднее арифметическое начальной и конечной скоростей на заданном отрезке времени:

\

Ответ: При данном в условии задачи законе движения материальной точки средняя скорость может быть найдена как среднее арифметическое начальной скорости и конечной ($\left\langle v\right\rangle =\frac{v\left(t=0\right)+v\left(t=t’\right)}{2}$).

Траектория, радиус-вектор, закон движения тела

Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад  в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.

Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют

Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно

Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется

Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна

А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.

Радиус-вектор – вектор, задающий положение точки в пространстве.

Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат  (или радиус-вектора точки) от времени.